12. A(6,-8), B(6,1), C(7,-2), D(-2,-2) D-19 ARE A B 2 C D congruers
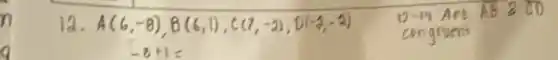
Solution4.4(265 votes)
Answer
Explanation
Similar Questions
4) Evaluate. Write your answer as a whole number or as a simplified fraction. $4^{3}\cdot 3^{2}=\square $
5 Cheddar cheese costs $\$ 4.25$ per pound. Which equation best represents y, the total cost of x pounds of cheddar cheese? Your answer
Simplify. $\frac {\frac {9}{2}-6}{1+\frac {7}{6}}$ $\square $
Find the partial sum. $\{ 38,31,24,17,\ldots \} ;S_{12}$
7. Find the coordinates of the intersection of the diagonals of the parallelogram with vertices $(-2,-4),(-4,4),(2,12)$ and $(4,4)$ 8. Three vertices of $\square ABCD$ are $A(1,5),B(1,1)$ and $D(2,2)$ Find the coordinates of the remaining vertex.
The GCF of $40c^{6}$ and $48c^{7}$ is $8c$ The missing exponent is __ The solution is $\square $
Find the solution(s) to each equation, or explain why there is no solution. $\sqrt {x+4}+7=5$
28. \( \left(\frac{112}{7}\right)^{\frac{1}{4}} \)
use the distributive property to remove the parentheses. $(2z^{4}-8z^{3}+3)4z^{5}$ Simplify your answer as much as possible.
$Area=4\cdot 69$ $=\square \cdot (\square -\square )$









