(1 point)Divide x^5-3x^4-23x^3+51x^2+94x-120b x^2-4x+3 Answer: square x^3+square x^2+square x+ square
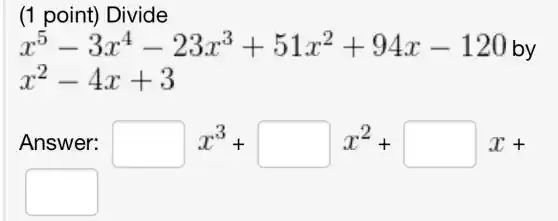
Solution4.2(152 votes)
Answer
Explanation
Similar Questions
5 Multiple Choice 20 points Suppose you have a right triangle called $\Delta MNP$ where $\angle N$ is the right angle. If $MN=6$ and $MP=17$ which can be used to find $m\angle P$ $arccos(\frac {6}{17})$ $arccos(\frac {17}{6})$ $arctan(\frac {17}{6})$ $arcsin(\frac {6}{17})$
Find the sum of the geometric series. $-3-12-48-192,\ldots n=6$ $-3320$ $-4095$ 1 $-3692$
29. A student incorrectly simplifies an expression.The expression and the student's work are shown below. $5-(\frac {40}{5})$ Step A: $5+(\frac {-40}{-5})$ Step B: $5+8$ Step C: 13 In which step did the student first make an error? Be sure to include the correct value of the expression in simplest form in your answer. Explain your answer.
Find the next three terms in the sequence. $9,12,16,21,\ldots $ $27,34,39$ $27,34,42$ $27,34,46$ $27,34,47$
6. The city zoo has different admission prices for adults and children . When 3 adults and 2 children went to the zoo, the bill was $\$ 78.34$ If 2 adults and 3 children went, the bill was $\$ 73.91$ Find the price for adult and child.
Question 6 of 10 It is always helpful to rewrite a quadratic equation in standard form as a first step in solving it. A. FALSE B. TRUE
Compute the derivative of the function $f(x)=(\frac {3x^{2}-x+1}{x^{2}+1})^{7}$ Select one: a $7(\frac {3x^{2}-x+1}{x^{2}+1})^{6}$ b. $7(\frac {3x^{2}-x+1}{x^{2}+1})^{6}\cdot \frac {x^{2}+4x-1}{(x^{2}+1)^{2}}$ C. $7(\frac {3x^{2}-x+1}{x^{2}+1})^{6}\cdot \frac {1}{(x^{2}+1)^{2}}$ d. $(\frac {3x^{2}-x+1}{x^{2}+1})^{6}\cdot \frac {x^{2}+4x-1}{(x^{2}+1)^{2}}$
Find the domain of $y=log(1-5x)$ The domain is: $\square $
The sum of the first four terms of a geometric series with a first term of 2 and a common ratio of 4 is 136. True False
For which of the following sample proportion distributions does the Central Limit Theorem apply? $n=20\hat {p}=0.3$ $n=20\hat {p}=0.2$ $n=20\hat {p}=0.8$ $n=20\hat {p}=0.1$









