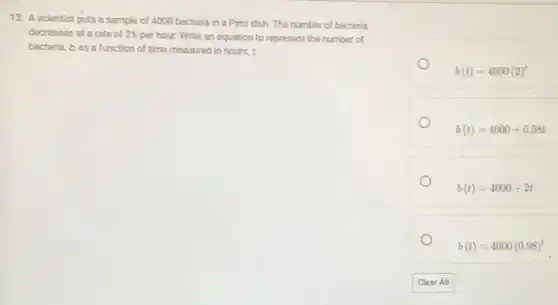
13. A scientist puts a sample of 4000 bacteria in a Petri dish The number of bacteria decreases at a rate of 2% per hour. Write an equation to represent the number of bacteria, b, as a function of time measured in hours, t. b(t)=4000(2)^t b(t)=4000+0.98t b(t)=4000+2t b(t)=4000(0.98)^t
Solution4.3(292 votes)
Answer
Explanation
Similar Questions
If your blood thickens the heart doesn't have to work as hard pumping the blood through your body. True False
Multiple Cholce Question Which of the following about classifying viruses is FALSE? An online database classifying viruses is kept by the ICTV (International Committee on Taxonomy of Viruses) Viruses can be classified based on different viral characteristics. It provides a useful way to identify and study viruses. It is not as important as classifying organisms since they are not living entities.
Question 1 Match the description with the pathogen: \begin{array}{|l|l|} \hline Candida\ albicans\ &\ [Choose]\ \\ \hline Trichomonas\ &\ [Choose]\ \\ \hline Histoplasmosis\ capsulatum\ &\ [Choose]\ \\ \hline Aspergillus\ &\ [Choose]\ \\ \hline \end{array}
Strata granulosum is abundant with which cell? Dendrocytes Keratinocytes Melanocytes
Which of the following is dominated by adipose tissue? Epidermis Hypodermis Dermis
Which of the following are described as partially encapsulated lymph tissue located in the throat? palatine tonsils pharyngeal tonsils lingual tonsils Peyer's Patches
Which of the following is not a function of proteins in the body? Serving as cofactors for enzymes Maintaining blood viscosity and osmolarity Muscle contraction Catalyzing enzymatic reactions Transport of blood lipids
Which sweat glands are only found in restricted areas? Sebaceous gland Merocrine gland Apocrine gland
Great. The flame kills all the microbes and sterilizes the wire loop.Why is this important to do before working with the chicken farm sample? a) To avoid contamination b) Salmonella can be found everywhere c) To reduce the spread of antibiotic resistance d) All the answers are correct
26. How is the DNA of a mouse different from the DNA of a snake? A. Only the DNA of the mouse contains nitrogen bases. B. The DNA molecules have different base sequences. C. The DNA of a mouse does not contain adenine. D. Only the DNA of a snake contains thymine.









