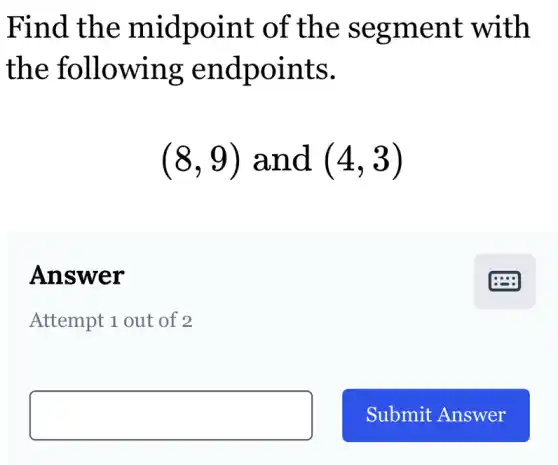
Find the midpoint of the segment with the following endpoints. (8,9) and (4,3) Answer Attempt 1 out of 2
Solution3.5(190 votes)
Answer
Explanation
Similar Questions
What is the next fraction in this sequence? $\frac {1}{48}$ $\frac {2}{48}$ $\frac {4}{48}$ $\frac {8}{48}$ __ $\square $
Serenity uses the following polynomial expression $x(x+5)(x-7)$ to model the volume of a rectangular prism.The height is shorter than the width and the length. What is the height of this prism? A. x ) B. $x-7$ C. $x+5$ D. $x^{3}-2x^{2}-35x$
Simplify each through multiplication/division. 9 $\frac {n^{2}+5n+6}{n^{2}+n-2}+\frac {n-1}{2n-2}$ 10) $\frac {x^{2}+2x-3}{3x-3}\cdot \frac {3x+6}{x+3}$ 11) $\frac {3x^{3}-6x^{2}}{3x^{2}+9x}\cdot \frac {x^{2}+4x+3}{3x^{3}+3$ 12) $\frac {2k+4}{k+2}\div \frac {k^{2}+3k+2}{k^{2}+4k+3}$
What is the prime factorization of 203? $7\times 29$ $7\times 7\times 29$ $7\times 203$ $7\times 29\times 29$
27) Rationalize the denominator to simplify the following expression. $\frac {4\sqrt {15}}{1+2\sqrt {5}}$
Which ordered pairs represent points on the graph of this equation?Select all th $2x+y=0$ $(1,-2)$ $(3,-6)$ $(-2,4)$ $(-3,6)$ $(-1,2)$ $(2,-4)$
Solve the following inequality for h. Write your answer in simplest form. $6h+4\leqslant -2h+5$ Answer Attempt 1 out of 4 $h\leqslant \vee \square $ Submit Answer
4) Evaluate the indefinite intergal \( \int\left(x^{-\frac{1}{2}}\right) d x \)
12. Bruce says that if a number is a product of 6, then it is not a product of 3. What would you say to Bruce?
What value of s is a solution to this equation? $-\frac {3+5}{2}=-7$ $s=3$ $s=11$









